Ministerio del Poder Popular Para la Educación
Unidad Educativa Prof.: "Fernando Ramirez"
Independencia - Yaracuy
Daniela Gonzales
Genesis Oca
Carlin Sanchez
Yanez Rosnelly
José D'onofrio
Jose Meza
Docente: Oly Mar Valenzuela
El movimiento rectilíneo uniformemente variado es aquel que experimenta aumentos o disminuciones y además la trayectoria es una línea recta Por tanto, unas veces se mueve más rápidamente y posiblemente otras veces va más despacio. En este caso se
Por tanto cabe mencionar que si la velocidad aumenta el movimiento es acelerado, pero si la velocidad disminuye es retardado
La representación Gráfica Es Una Parábola y existen dos Alternativas:
A) Si La Parábola Presenta Concavidad Positiva (Simulando La Posición De Una "U"), El Movimiento Se Denomina Movimiento Uniformemente Acelerado (M.U.A.).
B) Si La Parábola Presenta Concavidad Negativa ("U" Invertida), El Movimiento Se Denomina: Movimiento Uniformemente Retardado (M.U.R.).
Esta parábola describe la relacion que existe entre el tiempo y la distancia, ambos son directamente proporcionales a la un medio; y ese es el objetivo principal en que se basa el modelo de hipótesis de
S e puede interpretar que en el MRUV La velocidad se mantiene constante a lo largo del tiempo.
Observación:
Al colocar una esfera de acero sobre un plano inclinado; observamos que en su desplazamiento la distancia es directamente proporcional al tiempo.
Magnitudes físicas:
Problema definitivo:
Investigar la relación que existe entre el tiempo y la distancia recorrida por una esfera cuando es soltada del punto más alto de un plano inclinado.
Hipótesis Definitiva:
El tiempo es directamente proporcional a la distancia elevada a la un medio (1/2)
![]()
VARIABLE INDEPENDIENTE: Distancia
VARIABLE DEPENDIENTE: Tiempo
PARÁMETROS CONSTANTES: Gravedad,
MAGNITUDES DE INFLUENCIA: Temperatura
APROXIMACIONES: El 10 % de incertidumbre, la exactitud y la precisión de el
Objetivo
El objetivo de este trabajo experimental es determinar la aceleración de la caída de un cuerpo en el campo gravitatorio.
Procedimiento
El experimento consistió en determinar la aceleración con la que el elemento caía al piso, luego de ser arrojado desde una ventana.
Para esto primero necesitamos determinar la altura a la cual el cuerpo (en este caso una bolita de vidrio) seria arrojado. La altura era de 4.65 mts.
Un integrante de nuestro grupo que se encontraba en el patio, cuya altura tomamos como 0 mts., tenia un cronómetro con el cual iba a tomar el tiempo que empleaba la bolita para llegar al piso.
Mientras tanto, otra integrante del grupo se encontraba desde el lugar donde el cuerpo sería arrojado, preparada para lanzarlo. En el instante en el que ésta soltaba la bolita, la integrante que se encontraba abajo ponía en funcionamiento el cronómetro, para luego ser detenido en el momento en el que la bolita tocaba el piso.
Este procedimiento fue repetido cinco veces para poder calcular la aceleración de la gravedad.
Ecuaciones Utilizadas
1- Para calcular la gravedad máxima:
Gmax= 2 x Yo .
(t-0,05 seg.)²
2- Para calcular la gravedad mínima:
Gmin= 2 x Yo .
(t + 0,05 seg.) ²
3- Para calcular el error:
E= Gmax - Gmin
2
4- Para calcular el error promedio:
_
E= E1 + E2 + E3 + E4 + E5
Nº de tiros (5)
5- Para calcular la gravedad:
G= 2 x Yo
t²
6- Para calcular la gravedad promedio:
_
G= G1 + G2 + G3 + G4 + G5
Nº de tiros (5)
7- Para calcular la aceleración de la gravedad:
Un agujero negro u hoyo negro es una región finita del espacio-tiempo provocada por una gran concentración de masa en su interior, con enorme aumento de la densidad, lo que genera un campo gravitatorio tal que ninguna partícula material, ni siquiera los fotones de luz, puede escapar de dicha región.
La curvatura del espacio-tiempo o «gravedad de un agujero negro» provoca una singularidad envuelta por una superficie cerrada, llamada horizonte de sucesos. Esto es debido a la gran cantidad de energía del objeto celeste. El horizonte de sucesos separa la región del agujero negro del resto del Universo y es la superficie límite del espacio a partir de la cual ninguna partícula puede salir, incluyendo la luz. Dicha curvatura es estudiada por la relatividad general, la que predijo la existencia de los agujeros
Un agujero negro u hoyo negro es una región finita del espacio-tiempo provocada por una gran concentración de masa en su interior, con enorme aumento de la densidad, lo que genera un campo gravitatorio tal que ninguna partícula material, ni siquiera los fotones de luz, puede escapar de dicha región.
La curvatura del espacio-tiempo o «gravedad de un agujero negro» provoca una singularidad envuelta por una superficie cerrada, llamada horizonte de sucesos. Esto es debido a la gran cantidad de energía del objeto celeste. El horizonte de sucesos separa la región del agujero negro del resto del Universo y es la superficie límite del espacio a partir de la cual ninguna partícula puede salir, incluyendo la luz. Dicha curvatura es estudiada por la relatividad general, la que predijo la existencia de los agujeros negros y fue su primer indicio. En los años 70, Hawking, Ellis y Penrose demostraron varios teoremas importantes sobre la ocurrencia y geometría de los agujeros negros.[1] Previamente, en 1963, Roy Kerr había demostrado que en un espacio-tiempo de cuatro dimensiones todos los agujeros negros debían tener una geometría cuasi-esférica determinada por tres parámetros: su masa M, su carga eléctrica total e y su momento angular L.
Se cree que en el centro de la mayoría de las galaxias, entre ellas la Vía Láctea, hay agujeros negros supermasivos. La existencia de agujeros negros está apoyada en observaciones astronómicas, en especial a través de la emisión de rayos X por estrellas binarias y galaxias activas.
negros y fue su primer indicio. En los años 70, Hawking, Ellis y Penrose demostraron varios teoremas importantes sobre la ocurrencia y geometría de los agujeros negros.[1] Previamente, en 1963, Roy Kerr había demostrado que en un espacio-tiempo de cuatro dimensiones todos los agujeros negros debían tener una geometría cuasi-esférica determinada por tres parámetros: su masa M, su carga eléctrica total e y su momento angular L.
Se cree que en el centro de la mayoría de las galaxias, entre ellas la Vía Láctea, hay agujeros negros supermasivos. La existencia de agujeros negros está apoyada en observaciones astronómicas, en especial a través de la emisión de rayos X por estrellas binarias y galaxias activas.
Sus padres vivían en Londres, y fue en esa ciudad donde su padre se dedicó a la investigación médica. Durante la Segunda Guerra Mundial Londres era un lugar peligroso, y la madre de Stephen fue enviada a la ciudad de Oxford, donde él nació. La familia pronto regresó a Highgate, al norte de Londres, donde Stephen inició sus estudios.
En 1950 su padre se trasladó al Instituto de Investigación Médica de Mill Hill. Stephen asistió al Instituto para chicas de St Albans (que admitía chicos hasta la edad de 10 años) y a los 11 años cambió al Colegio homónimo. Su padre quería que se presentase a la convocatoria de beca para ir la Escuela Pública de Westminster, sin embargo Stephen estuvo enfermo durante el periodo de los exámenes.
En marzo de 1959 Hawking se presentó a las convocatorias de becas con el propósito de estudiar Ciencias Naturales en Oxford; consigue una beca, y se licencia en Física en 1962. Desde Oxford, Hawking se trasladó a Cambridge para iniciar la investigación en relatividad general y cosmología; unas áreas difíciles para alguien con poca base matemática. En aquel tiempo, Hawking había notado que se había vuelto más torpe y físicamente débil, y en la Navidad de 1962 su madre lo convenció para que viese a un médico.
A principios de 1963, pasó dos semanas haciéndose pruebas en el hospital, donde le diagnosticaron una enfermedad neuronal motora: la esclerosis lateral amiotrófica o enfermedad de Lou Gehrig. Su estado se deterioró rápidamente y los médicos le pronosticaron que no viviría lo suficiente para acabar su doctorado. Sin embargo, Hawking escribió:
Siguió su investigación porque encontró el estímulo de conocer a una chica con la que quería casarse y se dio cuenta que tenía que acabar su doctorado para conseguir un mejor trabajo.
Tras acabar su doctorado en 1966, Hawking consiguió una beca en Cambridge. Al principio, su trabajo fue de investigador, pero más tarde se convirtió en profesor. En 1973, dejó el Instituto de Astronomía y se unió al Departamento de Matemáticas Aplicadas y Física Teórica en Cambridge. Fue Profesor de Física Gravitacional en Cambridge en 1977. En 1979 Hawking fue nombrado Catedrático Lucasiano de Matemáticas en Cambridge; la cátedra de Newton en Cambridge; honor también compartido por Dirac.
Entre 1965 y 1970, Hawking trabajó en concreto en la Teoría General de la Relatividad ideando nuevas técnicas matemáticas para estudiarla. Gran parte de su trabajo lo hizo en colaboración con Roger Penrose.
Desde 1970, Hawking empezó a aplicar sus ideas previas al estudio de los agujeros negros y descubrió una propiedad notable: usando la Teoría Cuántica y la Relatividad General fue capaz de demostrar que los agujeros negros pueden emitir radiación. El éxito al confirmarlo le hizo trabajar a partir de aquel momento en la unificación de ambas, la relatividad general y la teoría cuántica. En 1971 Hawking investigó la creación del Universo y pronosticó que, después del Big Bang, se crearon muchos objetos supermasivos (del orden de 109 ton) del tamaño de un protón. Estos mini-agujeros negros poseían una gran atracción gravitacional controlada por la relatividad general, regida también por leyes de la mecánica cuántica que se aplicarían a objetos pequeños.
Otro éxito notable de Hawking fue su propuesta de una topología "sin fronteras" del Universo formulada en 1983 junto a Jim Hartle. Hawking lo explica así:
Ya en 1982, Hawking decide escribir un libro divulgativo de Cosmología: "Breve Historia del Tiempo". Sin embargo, Hawking sufre otro ataque:
A Hawking se le proporcionó un sistema informático para permitir que tuviese una voz electrónica.
Finalmente en 1988 se publicó "Una Breve Historia del Tiempo". El libro batió récords de ventas de una forma difícil de predecir. Como no podía ser de otra manera, Hawking ha recibido gran cantidad de honores; fue elegido miembro de Real Sociedad de Londres en 1974, siendo uno de los más jóvenes, también es miembro de la Academia Nacional de Ciencias de Estados Unidos. Se le fue concedido el CBE3 en 1982 y fue nombrado Compañero de Honor en 1989, mismo año en que recibió el Premio Príncipe de Asturias. En el año 2008 recibió el premio Fonseca 2008 que se entregó por primera vez el día 27 de septiembre de 2008.
La física es una de las más antiguas disciplinas académicas, tal vez la más antigua a través de la inclusión de la astronomía. En los últimos dos milenios, la física había sido considerada sinónimo de la filosofía, la química, y ciertas ramas de la matemática y la biología, pero durante la Revolución Científica en el siglo XVI surgió para convertirse en una ciencia moderna, única por derecho propio. Sin embargo, en algunas esferas como la física matemática y la química cuántica, los límites de la física siguen siendo difíciles de distinguir.
La física es significativa e influyente, no sólo debido a que los avances en la comprensión a menudo se han traducido en nuevas tecnologías, sino también a que las nuevas ideas en la física a menudo resuenan con las demás ciencias, las matemáticas y la filosofía.
La física no es sólo una ciencia teórica; es también una ciencia experimental. Como toda ciencia, busca que sus conclusiones puedan ser verificables mediante experimentos y que la teoría pueda realizar predicciones de experimentos futuros. Dada la amplitud del campo de estudio de la física, así como su desarrollo histórico en relación a otras ciencias, se la puede considerar la ciencia fundamental o central, ya que incluye dentro de su campo de estudio a la química, la biología y la electrónica, además de explicar sus fenómenos.
La física, en su intento de describir los fenómenos naturales con exactitud y veracidad, ha llegado a límites impensables: el conocimiento actual abarca la descripción de partículas fundamentales microscópicas, el nacimiento de las estrellas en el universo e incluso conocer con una gran probabilidad lo que aconteció en los primeros instantes del nacimiento de nuestro universo, por citar unos pocos campos.
Esta tarea comenzó hace más de dos mil años con los primeros trabajos de filósofos griegos como Demócrito, Epicuro o Aristóteles, y fue continuada después por científicos como Galileo Galilei, Isaac Newton, James Clerk Maxwell, Albert Einstein, Niels Bohr, Werner Heisenberg, Paul Dirac y Richard Feynman, entre muchos otros.
Albert Einstein (Ulm, Alemania, 14 de marzo de 1879 – Princeton, Estados Unidos, 18 de abril de 1955) fue un físico de origen alemán, nacionalizado posteriormente suizo y estadounidense. Está considerado como el científico más importante del siglo XX, además de ser el más conocido.[1]
En 1905, siendo un joven físico desconocido, que estaba empleado en la Oficina de Patentes de Berna, en (Suiza), publicó su teoría de la relatividad especial. En ella incorporó, en un marco teórico simple, fundamentado en postulados físicos sencillos, conceptos y fenómenos estudiados anteriormente por Henri Poincaré y por Hendrik Lorentz. Probablemente, la ecuación más conocida de la física a nivel popular, es la expresión matemática de la equivalencia masa-energía, E=mc², deducida por él como una consecuencia lógica de esta teoría. Ese mismo año publicó otros trabajos que sentarían algunas de las bases de la física estadística y la mecánica cuántica.
En 1915[2] presentó la Teoría General de la Relatividad, en la que reformuló por completo el concepto de gravedad. Una de las consecuencias fue el surgimiento del estudio científico del origen y evolución del Universo por la rama de la física denominada cosmología. En 1919, cuando las observaciones británicas de un eclipse solar confirmaron sus predicciones acerca de la curvatura de la luz, fue idolatrado por la prensa.[3] Einstein se convirtió en un icono popular de la ciencia mundialmente famoso, un privilegio al alcance de muy pocos científicos.[1]
Por sus explicaciones sobre el efecto fotoeléctrico y sus numerosas contribuciones a la física teórica, en 1921 obtuvo el Premio Nobel de Física y no por la Teoría de la Relatividad, pues el científico a quien se encomendó la tarea de evaluarla, no la entendió, y temieron correr el riesgo de que posteriormente se demostrase que fuese errónea.[4] [5] En esa época era aún considerada un tanto controvertida por parte de muchos científicos.
Ante el ascenso del nazismo en diciembre de 1932, el científico abandonó Alemania con destino a Estados Unidos, donde impartió docencia en el Instituto de Estudios Avanzados de Princeton. Se nacionalizó estadounidense en 1940. Durante sus últimos años trabajó por integrar en una misma teoría las cuatro Fuerzas Fundamentales. Murió en Princeton, Nueva Jersey, el 18 de abril de 1955.
Curiosamente, fue el astrofísico inglés Fred Hoyle, uno de los detractores de esta teoría y, a su vez, uno de los principales defensores de la teoría del estado estacionario, quien dijo para mofarse que el modelo descrito era sólo un big bang (gran explosión) durante una discusión de la BBC en 1949. No obstante, hay que tener en cuenta que en el inicio del Universo ni hubo explosión ni fue grande, pues en rigor surgió de una «singularidad» infinitamente pequeña, seguida de la expansión del propio espacio.[1]
La idea central del Big Bang es que la teoría de la relatividad general puede combinarse con las observaciones de isotropía y homogeneidad a gran escala de la distribución de galaxias y los cambios de posición entre ellas, permitiendo extrapolar las condiciones del Universo antes o después en el tiempo.
Una consecuencia de todos los modelos de Big Bang es que, en el pasado, el Universo tenía una temperatura más alta y mayor densidad y, por tanto, las condiciones del Universo actual son muy diferentes de las condiciones del Universo pasado. A partir de este modelo, George Gamow en 1948 pudo predecir que debería de haber evidencias de un fenómeno que más tarde sería bautizado como radiación de fondo de microondas
Basándose en medidas de la expansión del Universo utilizando observaciones de las supernovas tipo 1a, en función de la variación de la temperatura en diferentes escalas en la radiación de fondo de microondas y en función de la correlación de las galaxias, la edad del Universo es de aproximadamente 13,7 ± 0,2 miles de millones de años. Es notable el hecho de que tres mediciones independientes sean consistentes, por lo que se consideran una fuerte evidencia del llamado modelo de concordancia que describe la naturaleza detallada del Universo.
El universo en sus primeros momentos estaba lleno homogénea e isótropamente de una energía muy densa y tenía una temperatura y presión concomitantes. Se expandió y se enfrió, experimentando cambios de fase análogos a la condensación del vapor o a la congelación del agua, pero relacionados con las partículas elementales.
Aproximadamente 10-35 segundos después del tiempo de Planck un cambio de fase causó que el Universo se expandiese de forma exponencial durante un período llamado inflación cósmica. Al terminar la inflación, los componentes materiales del Universo quedaron en la forma de un plasma de quarks-gluones, en donde todas las partes que lo formaban estaban en movimiento en forma relativista. Con el crecimiento en tamaño del Universo, la temperatura descendió, y debido a un cambio aún desconocido denominado bariogénesis, los quarks y los gluones se combinaron en bariones tales como el protón y el neutrón, produciendo de alguna manera la asimetría observada actualmente entre la materia y la antimateria. Las temperaturas aún más bajas condujeron a nuevos cambios de fase, que rompieron la simetría, así que les dieron su forma actual a las fuerzas fundamentales de la física y a las partículas elementales. Más tarde, protones y neutrones se combinaron para formar los núcleos de deuterio y de helio, en un proceso llamado nucleosíntesis primordial. Al enfriarse el Universo, la materia gradualmente dejó de moverse de forma relativista y su densidad de energía comenzó a dominar gravitacionalmente sobre la radiación. Pasados 300.000 años, los electrones y los núcleos se combinaron para formar los átomos (mayoritariamente de hidrógeno). Por eso, la radiación se desacopló de los átomos y continuó por el espacio prácticamente sin obstáculos. Ésta es la radiación de fondo de microondas.
Al pasar el tiempo, algunas regiones ligeramente más densas de la materia casi uniformemente distribuida crecieron gravitacionalmente, haciéndose más densas, formando nubes, estrellas, galaxias y el resto de las estructuras astronómicas que actualmente se observan. Los detalles de este proceso dependen de la cantidad y tipo de materia que hay en el Universo. Los tres tipos posibles se denominan materia oscura fría, materia oscura caliente y materia bariónica. Las mejores medidas disponibles (provenientes del WMAP) muestran que la forma más común de materia en el universo es la materia oscura fría. Los otros dos tipos de materia sólo representarían el 20 por ciento de la materia del Universo.
El Universo actual parece estar dominado por una forma misteriosa de energía conocida como energía oscura. Aproximadamente el 70 por ciento de la densidad de energía del universo actual está en esa forma. Una de las propiedades características de este componente del universo es el hecho de que provoca que la expansión del universo varíe de una relación lineal entre velocidad y distancia, haciendo que el espacio-tiempo se expanda más rápidamente que lo esperado a grandes distancias. La energía oscura toma la forma de una constante cosmológica en las ecuaciones de campo de Einstein de la relatividad general, pero los detalles de esta ecuación de estado y su relación con el modelo estándar de la física de partículas continúan siendo investigados tanto en el ámbito de la física teórica como por medio de observaciones.
Más misterios aparecen cuando se investiga más cerca del principio, cuando las energías de las partículas eran más altas de lo que ahora se puede estudiar mediante experimentos. No hay ningún modelo físico convincente para el primer 10-33 segundo del universo, antes del cambio de fase que forma parte de la teoría de la gran unificación. En el "primer instante", la teoría gravitacional de Einstein predice una singularidad gravitacional en donde las densidades son infinitas. Para resolver esta paradoja física, hace falta una teoría de la gravedad cuántica. La comprensión de este período de la historia del universo figura entre los mayores problemas no resueltos de la física.
Dimensiones de esta vista previa: 800 × 576 píxelesUn movimiento es rectilíneo cuando el móvil describe una trayectoria recta, y es uniforme cuando su velocidad es constante en el tiempo, dado que su aceleración es nula. Nos referimos a él mediante el acrónimo MRU.
El MRU (movimiento rectilíneo uniforme) se caracteriza por:
características
La distancia recorrida se calcula multiplicando la magnitud de la velocidad (celeridad o rapidez) por el tiempo transcurrido. Esta relación también es aplicable si la trayectoria no es rectilínea, con tal que la celeridad o módulo de la velocidad sea constante.
La celeridad puede ser nula (reposo), positiva o negativa. Por lo tanto el movimiento puede considerarse en dos sentidos; una celeridad negativa representa un movimiento en dirección contraria al sentido que convencionalmente hayamos adoptado como positivo.
De acuerdo con la Primera Ley de Newton, toda partícula permanece en reposo o en movimiento rectilíneo uniforme cuando no hay una fuerza neta que actúe sobre el cuerpo. Esta es una situación ideal, ya que siempre existen fuerzas que tienden a alterar el movimiento de las partículas, por lo que en el movimiento rectilíneo uniforme es difícil encontrar la fuerza amplificada.

La física es la ciencia que se ocupa de los componentes fundamentales del Universo, de las fuerzas que éstos ejercen entre sí y de los efectos de dichas fuerzas. En ocasiones la física moderna incorpora elementos de los tres aspectos mencionados, como ocurre con las leyes de simetría y conservación de la energía, el momento, la carga o la paridad. La física está estrechamente relacionada con las demás ciencias naturales, y en cierto modo las engloba a todas
La rapidez es una magnitud escalar que relaciona la distancia recorrida con el tiempo a diferencia de la velocidad que es una magnitud vectorial que relaciona el cambio de posición (o desplazamiento) con el tiempo
El movimiento es un fenómeno
Entre los elementos del movimiento Tenemos:
La trayectoria. Es la línea que describe un cuerpo en movimiento. Atendiendo a su trayectoria los movimientos, puede ser: Rectilíneos, Curvilíneos, Elíptico, Parabólico
La distancia. Es la longitud comprendida entre el origen del movimiento y la posición
Velocidad: Es la distancia recorrida en la unidad de tiempo.
Tiempo: Lo que tarda en efectuarse el movimiento.
Es la ciencia que se ocupa de los componentes fundamentales del Universo, de las fuerzas que éstos ejercen entre sí y de los efectos de dichas fuerzas. En ocasiones la física moderna incorpora elementos de los tres aspectos mencionados, como ocurre con las leyes de simetría y conservación de la energía, el momento, la carga o la paridad.La física está estrechamente relacionada con las demás ciencias naturales, y en cierto modo las engloba a todas. Estudia los procesos de la naturaleza desde un punto de vista energético, cinemático o estadístico. Tiene dos fines principalmente: averiguar y comprender las causas de los sucesos, y predecir los sucesos provocados por dichas causas.
Es la rama de la mecánica clásica que estudia las leyes del movimiento de los cuerpos sin tener en
Es un fenómeno físico que se define como todo cambio de posición que experimentan los cuerpos en el espacio, con respecto al tiempo y a un punto de referencia, variando la distancia de dicho cuerpo con respecto a ese punto o sistema de referencia, describiendo una trayectoria. Para producir movimiento es necesaria una intensidad de interacción o intercambio de energía que sobrepase un determinado umbral.
Cuales son los elementos del movimiento
La trayectoria. Es la línea que describe un cuerpo en movimiento. Atendiendo a su trayectoria los movimientos, puede ser:
Rectilíneos: describen una línea recta.
Curvilíneos: Circular: describe una circunferencia
Elíptico: describe una elipse.
Parabólico: describe una parábola.
La distancia. Es la longitud comprendida entre el origen del movimiento y la posición final.
Velocidad: Es la distancia recorrida en la unidad de tiempo.
Tiempo: Lo que tarda en efectuarse el movimiento
Diferencia entre Rapidez y Velocidad
La rapidez: Es una magnitud escalar que relaciona la distancia recorrida con el tiempo.
La velocidad: Es una magnitud vectorial que relaciona el cambio de posición (o desplazamiento) con el tiempo.
Campo Vectorial: Es una función E que asocia a cada punto del espacio un vector, a diferencia de las funciones tradicionales, que asocian a cada punto del espacio un valor numérico. Un ejemplo de función tridimensional tradicional sería la presión atmosférica sobre la tierra: para cada punto geográfico (identificado con una longitud, latitud y altitud) existe un
Es un movimiento, determinado exclusivamente por fuerzas gravitatorias, que adquieren los cuerpos al caer, partiendo del reposo, hacia la superficie de la Tierra y sin estar impedidos por un medio que pudiera producir una fuerza de fricción o de empuje. Algunos ejemplos son el movimiento de la Luna alrededor de la Tierra o la caída de un objeto a la superficie terrestre.
En el vacío todos los cuerpos, con independencia de su forma o de su masa, caen con idéntica aceleración en un lugar determinado, próximo a la superficie terrestre. El movimiento de caída libre es un movimiento uniformemente acelerado, es decir, la aceleración instantánea es la misma en todos los puntos del recorrido y coincide con la aceleración media, y esta aceleración es la aceleración de la gravedad g = 9,8 m/s2. Como la velocidad inicial en el movimiento de caída libre es nula, las ecuaciones de la velocidad y el espacio recorrido en función del tiempo.
Se refiere a objetos en movimientos y es una magnitud vectorial que desempeña un papel muy importante en la segunda ley de Newton. La cantidad de movimiento combina las ideas de inercia y movimiento. También obedece a un principio de conservación que se ha utilizado para descubrir muchos hechos relacionados con las partículas básicas del Universo.
La ley de la conservación de la cantidad de movimiento y la ley de la conservación de la energía, son las herramientas más poderosas de la mecánica. La conservación de la cantidad de movimiento es la
Un vector es utilizado para representar una magnitud física el cual necesita de un módulo y una dirección (u orientación) para quedar definido.
Los vectores se pueden representar geométricamente como segmentos de recta dirigidos o flechas en planos  o
o  ; es decir, bidimensional o tridimensional.
; es decir, bidimensional o tridimensional.
Frente a aquellas magnitudes físicas, tales como la masa, la presión, el volumen, la energía, la temperatura, etc; que quedan completamente definidas por un número y las unidades utilizadas en su medida, aparecen otras, tales como el desplazamiento, la velocidad, la aceleración, la fuerza, el campo eléctrico, etc., que no quedan completamente definidas dando un dato numérico, sino que llevan asociadas una dirección. Estas últimas magnitudes son llamadas vectoriales en contraposición a las primeras que son llamadas escalares.
Las magnitudes escalares quedan representadas por el ente matemático más simple; por un número. Las magnitudes vectoriales quedan representadas por un ente matemático que recibe el nombre de vector. En un espacio euclidiano, de no más de tres dimensiones, un vector se representa por un segmento orientado. Así, un vector queda caracterizado por los siguientes elementos: su longitud o módulo, siempre positivo por definición, y su dirección, determinada por el ángulo que forma el vector con los ejes de coordenadas. Así pues, podemos enunciar:
Se representa como un segmento orientado, con una dirección o recta soporte del vector, dibujado de forma similar a una "flecha" en uno u otro sentido, su longitud representa el modulo del vector.[3]
Las magnitudes vectoriales se representan en los textos impresos por letras en negrita, para diferenciarlas de las magnitudes escalares que se representan en cursiva. En los textos manuscritos, las magnitudes vectoriales se representan colocando una flechita sobre la letra que designa su módulo (que es un escalar). Ejemplos:
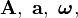 ... representan, respectivamente, las magnitudes vectoriales de módulos A, a, ω, ... El módulo de una magnitud vectorial también se representa encerrando entre barras la notación correspondiente al vector:
... representan, respectivamente, las magnitudes vectoriales de módulos A, a, ω, ... El módulo de una magnitud vectorial también se representa encerrando entre barras la notación correspondiente al vector: 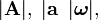 ...
...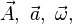 ... para los vectores y
... para los vectores y  ... o
... o 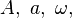 ... para los módulos.
... para los módulos.Cuando convenga, representaremos la magnitud vectorial haciendo referencia al origen y al extremo del segmento orientado que la representa geométricamente; así, designaremos los vectores representados en la Figura 2 en la forma  , ... resultando muy útil esta notación para los vectores desplazamiento.
, ... resultando muy útil esta notación para los vectores desplazamiento.
Además de estas convenciones los vectores unitarios o versores, cuyo módulo es la unidad, se representan frecuentemente con un circunflejo encima, por ejemplo  .
.
Según los criterios que se utilicen para determinar la igualdad o equipolencia de dos vectores, pueden distinguirse distintos tipos de los mismos:
Podemos referirnos también a:
Un vector en el espacio se puede expresar como una combinación lineal de tres vectores unitarios o versores perpendiculares entre sí que constituyen una base vectorial.
En coordenadas cartesianas, los vectores unitarios se representan por 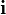 ,
, 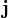 ,
, 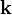 , paralelos a los ejes de coordenadas x, y, z positivos. Las componentes del vector en una base vectorial predeterminada pueden escribirse entre paréntesis y separadas con comas:
, paralelos a los ejes de coordenadas x, y, z positivos. Las componentes del vector en una base vectorial predeterminada pueden escribirse entre paréntesis y separadas con comas:
o expresarse como una combinación de los vectores unitarios definidos en la base vectorial. Así, en un sistema de coordenadas cartesiano, será
Estas representaciones son equivalentes entre sí, y los valores ax, ay, az, son las componentes de un vector que, salvo que se indique lo contrario, son números reales.
Una representación conveniente de las magnitudes vectoriales es mediante un vector columna o un vector fila, particularmente cuando están implicadas operaciones matrices (tales como el cambio de base), del modo siguiente:
Con esta notación, los versores cartesianos quedan expresados en la forma: