Potencia de igual Base

La potenciación es una expresión matemática que incluye dos términos denominados: base a y exponente n.

Se escribe aⁿ, y se lee: «a elevado a n». Su definición varía según el conjunto numérico al que pertenezca el exponente:

• Cuando el exponente es un número natural, equivale a multiplicar un número por sí mismo varias veces: el exponente determina la cantidad de veces.

Por ejemplo: .

• cuando el exponente es un número entero negativo, equivale a la fracción inversa de la base pero con exponente positivo.

• cuando el exponente es una fracción irreducible n/m, equivale a una raíz:

Cualquier número elevado a 0 equivale a 1, excepto el caso particular de 0⁰ que, en principio, es una indefinición.

La definición de potenciación puede extenderse a exponentes reales, complejos o incluso matriciales.

Potencia de exponente 0

Cualquier número elevado a 0, distinto de 0, es igual a 1

El caso especial 0⁰ se considera indefinido y dependiendo del contexto pueden ser asignados distintos valores dependiendo de las propiedades específicas que se quieran mantener.

Por ejemplo, puede argumentarse que 0⁰ es el igual al valor del límite

y como x⁰ = 1 para 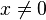, dicho valor podría ser igual a 1. Sin embargo también puede considerarse dicha expresión como el valor del límite

y como 0^x = 0 para 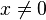, dicho valor podría ser igual a 0. Esto ilustra que la forma 0⁰ puede corresponde a diferentes valores y por ello se considera indefinida.

El debate sobre el valor de la forma 0⁰ tiene casi 2 siglos de antigüedad. Durante los primeros días del análisis matemático en que el fundamento formal del cálculo no se había establecido, era común aceptar que 0⁰=1. Sin embargo, en 1821 cuando Cauchy publica el Cours d'Analyse de l'École Royale Polytechnique estableciendo el primer tratamiento riguroso del análisis, lista dicha forma en una tabla de formas indefinidas junto a otras como 0/0. En los 1830s, Libri^{[1] [2]} publicó un argumento para asignar 1 como valor de 0⁰ y August Möbius^[3] lo apoyó afirmando erróneamente que

siempre que

Sin embargo un comentarista que firmó simplemente como «S» proporcionó un contraejemplo

cuyo límite cuando 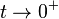es 1 / e, lo cual calmó el debate con la aparente conclusión del incidente que 0⁰ debería permanecer indefinida. Se pueden encontrar más detalles en Knuth (1992).^[4]

En la actualidad, suele considerarse la forma 0⁰ como indefinida y no se le asigna valor si no se tiene un contexto en el cual el valor asignado tenga sentido. ^{[5] [6] [7]}

Para calcular límites cuyo valor aparente es 0⁰ suele usarse la Regla de L'Hopital.